আমরা ষষ্ঠ শ্রেণিতে সমীকরণ ও সরল সমীকরণ কী তা জেনেছি এবং বাস্তবভিত্তিক সমস্যা থেকে সমীকরণ গঠন করে তা সমাধান করতে শিখেছি। সপ্তম শ্রেণির এ অধ্যায়ে আমরা সমীকরণ সমাধানের কিছু বিধি ও এদের প্রয়োগ সম্পর্কে জানব এবং বাস্তব সমস্যার ভিত্তিতে সমীকরণ গঠন করে তা সমাধান করা শিখব। এ ছাড়াও এ অধ্যায়ে লেখচিত্র সম্পর্কে প্রাথমিক ধারণা দেওয়া হয়েছে এবং সমীকরণের সমাধান লেখচিত্রে দেখানো হয়েছে।

অধ্যায় শেষে শিক্ষার্থীরা -

• সমীকরণের পক্ষান্তরবিধি, বর্জনবিধি, আড়গুণনবিধি, প্রতিসাম্যবিধি ব্যাখ্যা করতে পারবে।
• সমীকরণের বিধিসমূহ প্রয়োগ করে সমীকরণ সমাধান করতে পারবে।
• সরল সমীকরণ গঠন ও সমাধান করতে পারবে।
• লেখচিত্র কী তা ব্যাখ্যা করতে পারবে।
• লেখচিত্রের অক্ষ ও সুবিধাজনক একক নিয়ে বিন্দুপাতন করতে পারবে।
• লেখচিত্রের সাহায্যে সমীকরণের সমাধান করতে পারবে।

(১) যোগের ও গুণের বিনিময়বিধি

a, b এর যেকোনো মানের জন্য, a + b = b + a এবং ab = ba

(২) গুণের বণ্টনবিধি

a, b, c এর যেকোনো মানের জন্য, a(b + c) = ab + ac, (b + c) a = ba + ca

আমরা সমীকরণটি লক্ষ করি: x + 3 = 7

(ক) সমীকরণটির অজ্ঞাত রাশি বা চলক কোনটি?
(থ) সমীকরণটির প্রক্রিয়া চিহ্ন কোনটি?
(গ) সমীকরণটি সরল সমীকরণ কি না?
(ঘ) সমীকরণটির মূল কত?

আমরা জানি চলক, প্রক্রিয়া চিহ্ন ও সমান চিহ্ন সংবলিত গাণিতিক বাক্যকে সমীকরণ বলে। আর চলকের এক ঘাত বিশিষ্ট সমীকরণকে সরল সমীকরণ বলে। সরল সমীকরণ এক বা একাধিক চলকবিশিষ্ট হতে পারে।

যেমন, x + 3 = 7, 2y - 1 = y + 3, 3z - 5 = 0, 4 + 3 = x - 1,

x + 4y - 1 = 0, 2x - y + 1 = x + y ইত্যাদি, এগুলো সরল সমীকরণ।

আমরা এ অধ্যায়ে শুধু এক চলকবিশিষ্ট সরল সমীকরণ নিয়ে আলোচনা করব।

সমীকরণ সমাধান করে চলকের যে মান পাওয়া যায়, একে সমীকরণটির মূল বলে। মূলটি দ্বারা সমীকরণটি সিদ্ধ হয়। অর্থাৎ, চলকটির ঐ মান সমীকরণে বসালে সমীকরণটির দুইপক্ষ সমান হয়।

সমীকরণ সমাধানের জন্য চারটি স্বতঃসিদ্ধ আছে, তা আমরা জানি। এগুলো হলো:

• পরস্পর সমান রাশির প্রত্যেকটির সাথে একই রাশি যোগ করলে যোগফলগুলো পরস্পর সমান হয়।
• পরস্পর সমান রাশির প্রত্যেকটি থেকে একই রাশি বিয়োগ করলে বিয়োগফলগুলো পরস্পর সমান হয়।
• পরস্পর সমান রাশির প্রত্যেকটিকে একই রাশি দ্বারা গুণ করলে গুণফলগুলো পরস্পর সমান হয়।
• পরস্পর সমান রাশির প্রত্যেকটিকে অশূন্য একই রাশি দ্বারা ভাগ করলে ভাগফলগুলো পরস্পর সমান হয়।

(১) পক্ষান্তরবিধি

সমীকরণ-১ এ (খ) এর ক্ষেত্রে 5 এর চিহ্ন পরিবর্তিত হয়ে বামপক্ষ থেকে ডানপক্ষে গেছে। সমীকরণ-২ এ (খ) এর ক্ষেত্রে 3x এর চিহ্ন পরিবর্তিত হয়ে ডানপক্ষ থেকে বামপক্ষে গেছে।

উদাহরণ ১। সমাধান কর: x + 3 = 9

সমাধান: x + 3 = 9

বা, x = 9 - 3 [পক্ষান্তর করে]

বা, x = 6

∴ সমাধান: x = 6

(২) বর্জনবিধি

(a) যোগের বর্জনবিধি:

সমীকরণ-১ এ (খ) এর ক্ষেত্রে উভয়পক্ষ থেকে 3 বর্জন করা হয়েছে।

সমীকরণ-২ এ (খ) এর ক্ষেত্রে উভয়পক্ষ থেকে -5 বর্জন করা হয়েছে।

বিকল্প নিয়ম: x + 3 = 9

বা, x + 3 - 3 = 9 - 3 [উভয়পক্ষ থেকে 3 বিয়োগ করে]

বা, x = 6

∴ সমাধান: x = 6

(b) গুণের বর্জনবিধি

(খ) এর ক্ষেত্রে প্রদত্ত সমীকরণটির উভয়পক্ষ থেকে সাধারণ উৎপাদক সরাসরি বর্জন করা যায়।

উদাহরণ ২। সমাধান কর ও শুদ্ধি পরীক্ষা কর: 4y - 5 = 2y - 1

সমাধান: 4y - 5 = 2y - 1

বা, 4y - 2y = - 1 + 5 [পক্ষান্তর করে]

বা, 2y = 4

বা, 2y = 2 $\times$ 2

বা, y = 2 [উভয়পক্ষ থেকে সাধারণ উৎপাদক 2 বর্জন করে]

∴ সমাধান: y = 2

শুদ্ধি পরীক্ষা: প্রদত্ত সমীকরণে y এর মান 2 বসিয়ে পাই,

বামপক্ষ = 4y - 5 = 4 $\times$ 2 - 5 = 8 - 5 = 3

ডানপক্ষ = 2y - 1 = 2 $\times$ 2 - 1 = 4 - 1 = 3

∴ বামপক্ষ = ডানপক্ষ

∴ সমীকরণটির সমাধান শুদ্ধ হয়েছে।

(৩) আড়গুণনবিধি

সমীকরণটির (খ) এর ক্ষেত্রে লিখতে পারি,

উদাহরণ ৩। সমাধান কর: $\frac{2z}{3}-\frac{z}{6}=-\frac{3}{4}$

সমাধান:

$\frac{2z}{3}-\frac{z}{6}=-\frac{3}{4}$

বা, $\frac{4z-z}{6}=-\frac{3}{4}$[বামপক্ষে হর 3,6 এর ল.সা.গু. 6]

বা, $\frac{3z}{6}=-\frac{3}{4}$

বা, $\frac{z}{2}=-\frac{3}{4}$

বা, $4\times z = 2\times (- 3)$[আড়গুণন করে]

বা, $2 \times 2z = 2\times (- 3)$

বা, 2z = - 3 [উভয়পক্ষ থেকে সাধারণ উৎপাদক 2 বর্জন করে]

বা, $\frac{2z}{2}=-\frac{3}{2}$[উভয়পক্ষকে 2 দ্বারা ভাগ করে।]

বা, $z=-\frac{3}{2}$

∴ সমাধান: $z=-\frac{3}{2}$

(৪) প্রতিসাম্যবিধি

সমীকরণ: 2x + 1 = 5x - 8

বা, 5x - 8 = 2x + 1

একই সাথে বামপক্ষের সবগুলো পদ ডানপক্ষে ও ডানপক্ষের সবগুলো পদ বামপক্ষে কোনো চিহ্ন পরিবর্তন না করে স্থানান্তর করা যায়। একে বলা হয় প্রতিসাম্যবিধি।

উল্লিখিত স্বতঃসিদ্ধসমূহ ও বিধিসমূহ প্রয়োগ করে একটি সমীকরণকে অপর একটি সহজ সমীকরণে রূপান্তর করে সবশেষে তা x = a আকারে পাওয়া যায়। অর্থাৎ, চলক x এর মান a নির্ণয় করা হয়।

উদাহরণ ৪। সমাধান কর: 2(5 + x) = 16

সমাধান: 2(5 + x) = 16

বা, 2 $\times$ 5 + 2$\times$x = 16[বণ্টনবিধি অনুসারে

বা. 10 + 2x = 16

বা, 2x = 16 - 10 [পক্ষান্তরবিধি]

বা, 2x = 6

বা, $\frac{2x}{2}=\frac{6}{2}$[গুণের বণ্টনবিধি]

∴ সমাধান x = 3

উদাহরণ ৫। সমাধান কর:

$\frac{3x + 7}{4}+ \frac{5x - 4}{7} = x + 3\frac{1}{2}$

সমাধান:

$\frac{3x + 7}{4}+ \frac{5x - 4}{7} = x + 3\frac{1}{2}$

বা, $\frac{3x + 7}{4} + \frac{5x - 4}{7}- x =\frac{7}{2}$[পক্ষান্তর করে]

বা, $\frac{7(3x + 7) + 4(5x - 4) - 28x}{28} = \frac{7}{2}$[বামপক্ষে হর 4, 7 এর ল.সা.গু. 28]

বা, $\frac{21x + 49 + 20x - 16 - 28x}{28} = \frac{7}{2}$[বণ্টনবিধি অনুসারে]

বা, $\frac{13x + 33}{28} =\frac{7}{2}$

বা, $28 \times \frac{13x + 33}{28} = 28 \times \frac{7}{2}$ [উভয়পক্ষকে 28 দ্বারা গুণ করে]

বা, 13x + 33 = 98

বা, 13x = 98 - 33

বা, 13x = 65

বা, $\frac{13x}{13} =\frac{65}{13}$ [উভয়পক্ষকে 13 দ্বারা ভাগ করে।]

বা, x = 5

∴ সমাধান: x = 5

সমাধান কর:

১। 4x + 1 = 2x + 7 ২। 5x - 3 = 2x + 3

৩। 3y + 1 = 7y - 1 ৪। 7y - 5 = y - 1

৫। 17 - 2z = 3z + 2 ৬। 13z - 5 = 3 - 2z

৭। $\frac{x}{4}=\frac{1}{3}$ ৮। $\frac{x}{2}+1=3$

৯। $\frac{x}{3}+5=\frac{x}{2}+7$ ১০। $\frac{y}{2}-\frac{y}{3}=\frac{y}{5}-\frac{1}{6}$

১১। $\frac{y}{5}-\frac{2}{7}=\frac{5y}{7}-\frac{4}{5}$১২। $\frac{2z-1}{3}=5$

১৩। $\frac{5x}{7}+\frac{4}{5}=\frac{x}{5}+\frac{2}{7}$১৪। $\frac{y - 2}{4} + \frac{2y - 1}{3}= y - \frac{1}{3}$

১৫। $\frac{3y + 1}{5} = \frac{3y - 7}{3}$১৬। $\frac{x + 1}{2} - \frac{x - 2}{3}- \frac{x - 3}{5} = 2$

১৭। 2(x + 3) = 10 ১৮। 5(x - 2) = 3(x - 4)

১৯। 7(3 - 2y) + 5(y - 1) = 34 ২০। (z-1) (z + 2) = (z + 4)(z - 2)

একজন ক্রেতা 3 কেজি পাটালি গুড় কিনতে চান। দোকানদার x কেজি ওজনের একটি বড়ো পাটালির অর্ধেক মাপলেন। কিন্তু এতে 3 কেজির কম হলো। আরও 1 কেজি দেওয়ায় 3 কেজি হলো। আমরা এখন বের করতে চাই, বড়ো পাটালি অর্থাৎ সম্পূর্ণ পাটালিটির ওজন কত ছিল, অর্থাৎ x এর মান কত? এ জন্য সমস্যাটি থেকে একটি সমীকরণ গঠন করতে হবে। এক্ষেত্রে সমীকরণটি হবে $\frac{x}{2}+1=3$ । সমীকরণটি সমাধান করলে x এর মান পাওয়া যাবে। অর্থাৎ, গুড়ের সম্পূর্ণ পাটালির ওজন জানা যাবে।

উদাহরণ ৭। অহনা একটি পরীক্ষায় ইংরেজিতে ও গণিতে মোট 176 নম্বর পেয়েছে এবং ইংরেজি অপেক্ষা গণিতে 10 নম্বর বেশি পেয়েছে। সে কোন বিষয়ে কত নম্বর পেয়েছে?

সমাধান: ধরি, অহনা ইংরেজিতে x নম্বর পেয়েছে।

সুতরাং, সে গণিতে পেয়েছে (x+10) নম্বর।

প্রশ্নমতে,

x + x + 10 = 176

বা, 2x + 10 = 176

বা, 2x = 176 - 10 [পক্ষান্তর করে]

বা, 2x = 166

বা, $\frac{2x}{2}=\frac{166}{2}$[উভয়পক্ষকে 2 দ্বারা ভাগ করে]

বা, = 83

∴ x + 10 = 83 + 10 = 93

∴ অহনা ইংরেজিতে পেয়েছে 83 নম্বর এবং গণিতে পেয়েছে 93 নম্বর।

উদাহরণ ৮। শ্যামল দোকান থেকে কিছু কলম কিনল। সেগুলোর $\frac{1}{2}$অংশ তার বোনকে ও $\frac{1}{3}$অংশ তার ভাইকে দিল। তার কাছে আর 5 টি কলম রইল। শ্যামল কয়টি কলম কিনেছিল?

সমাধান: ধরি, শ্যামল Xটি কলম কিনেছিল।

∴ শ্যামল তার বোনকে দেয় x এর $\frac{1}{2}$টি বা $\frac{x}{2}$টি কলম এবং তার ভাইকে দেয় x এর $\frac{1}{3}$টি বা $\frac{x}{3}$টি কলম ।

শর্তানুসারে, $x-\left(\frac{x}{2}+\frac{x}{3}\right)=5$

বা, $x-\left(\frac{x}{2}+\frac{x}{3}\right)=5$

বা, $\frac{6x - 3x - 2x}{6} = 5$[বামপক্ষে হর 2,3 এর ল.সা.গু. 6]

বা, $\frac{x}{6}=5$

বা, x = 5 $\times$6 [আড়গুণন করে]

বা, x = 30

∴ শ্যামল 30 টি কলম কিনেছিল।

উদাহরণ ৯। একটি বাস ঘণ্টায় 25 কি.মি. গতিবেগে ঢাকার গাবতলী থেকে আরিচা পৌঁছাল। আবার বাসটি ঘণ্টায় 30 কি.মি. গতিবেগে আরিচা থেকে গাবতলী ফিরে এলো। যাতায়াতে বাসটির মোট $5\frac{1}{2}$ঘণ্টা সময় লাগল। গাবতলী থেকে আরিচার দূরত্ব কত?

সমাধান: মনে করি, গাবতলী থেকে আরিচার দূরত্ব d কি.মি.।

∴ গাবতলী থেকে আরিচা যেতে সময় লাগে $\frac{d}{25}$ঘণ্টা।

আবার আরিচা থেকে গাবতলী ফিরে আসতে সময় লাগে $\frac{d}{30}$ঘণ্টা।

∴ যাতায়াতে বাসটির মোট সময় লাগল $\left(\frac{d}{25}+\frac{d}{30}\right)$ঘণ্টা।

প্রশ্নমতে, $\frac{d}{25}+\frac{d}{30}=5\frac{1}{2}$

বা, $\frac{6d + 5d}{150} = \frac{11}{2}$

বা, $11d{=}^{75}\cancel{150} \times \frac{11}{{\cancel{2}}_1}$

বা, d = 75

∴ গাবতলী থেকে আরিচার দূরত্ব 75 কি.মি.।

উদাহরণ ১০। দুটি ধনাত্মক পূর্ণসংখ্যার অন্তর 40 এবং তাদের অনুপাত 1 : 3.

ক) সংখ্যা দুটিকে x ও y ধরে সমীকরণ গঠন কর।
খ) সংখ্যা দুটি নির্ণয় কর।
গ) সংখ্যা দুটিকে আয়তক্ষেত্রের দৈর্ঘ্য ও প্রস্থ এর একক মিটারে ধরে আয়তক্ষেত্রটির পরিসীমা ও ক্ষেত্রফল নির্ণয় কর।

সমাধান:

(ক) মনে করি, সংখ্যা দুটি x ও y

প্রশ্নমতে x-y=40 ………….. (i)

এবং y : x=1 : 3

বা, $\frac{y}{x}=\frac{1}{3}$

বা, x=3y ………….. (ii)

(খ) ক থেকে প্রাপ্ত

x - y = 40 …………… (i)

x = 3y ………………… (ii)

(i) ও (ii) নং থেকে পাই,

3y - y = 40

বা, 2y = 40

বা, $y =\frac{40}{2}$

∴ y = 20

(ii) নং y = 20 বসিয়ে পাই,

x = 3 $\times$ 20 = 60

∴ x = 60

∴ সংখ্যা দুটি 60 ও 20

গ) 'খ' থেকে প্রাপ্ত

সংখ্যা দুটি 60 ও 20 ।

ধরি, আয়তক্ষেত্রের দৈর্ঘ্য 60 মিটার

আয়তক্ষেত্রের প্রস্থ 20 মিটার

∴ আয়তক্ষেত্রটির পরিসীমা = 2 (দৈর্ঘ্য+প্রস্থ)

= 2(60+20) মিটার

= 2$\times$80 মিটার

=160 মিটার

আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য $\times$ প্রস্থ

= 60 মি. $\times$ 20 মি.

= 1200 ব.মি.

নিচের সমস্যাগুলো থেকে সমীকরণ গঠন করে সমাধান কর।

১। কোন সংখ্যার দ্বিগুণের সাথে 5 যোগ করলে যোগফল 25 হবে?

২। কোন সংখ্যা থেকে 27 বিয়োগ করলে বিয়োগফল 21 হবে?

৩। কোন সংখ্যার এক-তৃতীয়াংশ 4 এর সমান হবে?

৪। কোন সংখ্যা থেকে 5 বিয়োগ করলে বিয়োগফলের 5 গুণ সমান 20 হবে?

৫। কোন সংখ্যার অর্ধেক থেকে তার এক-তৃতীয়াংশ বিয়োগ করলে বিয়োগফল 6 হবে?

৬। তিনটি ক্রমিক স্বাভাবিক সংখ্যার সমষ্টি 63 হলে, সংখ্যা তিনটি বের কর।

৭। দুটি সংখ্যার যোগফল 55 এবং বড় সংখ্যাটির 5 গুণ ছোট সংখ্যাটির 6 গুণের সমান। সংখ্যা দুটি নির্ণয় কর।

৮। গীতা, রিতা ও মিতার একত্রে 180 টাকা আছে। রিতার চেয়ে গীতার 6 টাকা কম ও মিতার 12 টাকা বেশি আছে। কার কত টাকা আছে?

৯। একটি খাতা ও একটি কলমের মোট দাম 75 টাকা। খাতার দাম 5 টাকা কম ও কলমের দাম 2 টাকা বেশি হলে, খাতার দাম কলমের দামের দ্বিগুণ হতো। খাতা ও কলমের কোনটির দাম কত?

১০। একজন ফলবিক্রেতার মোট ফলের $\frac{1}{2}$অংশ আপেল, $\frac{1}{3}$অংশ কমলালেবু ও 40 টি আম আছে। তাঁর নিকট মোট কতগুলো ফল আছে?

১১। পিতার বর্তমান বয়স পুত্রের বর্তমান বয়সের 6 গুণ। 5 বছর পর তাদের বয়সের সমষ্টি হবে 45 বছর। পিতা ও পুত্রের বর্তমান বয়স কত?

১২। লিজা ও শিখার বয়সের অনুপাত 2:3। তাদের দুজনের বয়সের সমষ্টি 30 বছর হলে, কার বয়স কত?

১৩। একটি ক্রিকেট খেলায় ইমন ও সুমনের মোট রানসংখ্যা 58। ইমনের রানসংখ্যা সুমনের রানসংখ্যার দ্বিগুণের চেয়ে ১ রান কম। ঐ খেলায় ইমনের রানসংখ্যা কত?

১৪। একটি ট্রেন ঘণ্টায় 30 কি.মি. বেগে চলে কমলাপুর স্টেশন থেকে নারায়ণগঞ্জ স্টেশনে পৌঁছাল। ট্রেনটির বেগ ঘণ্টায় 25 কি.মি. হলে 10 মিনিট সময় বেশি লাগত। দুই স্টেশনের মধ্যে দূরত্ব কত?

১৫। একটি আয়তাকার জমির দৈর্ঘ্য প্রস্থের তিনগুণ এবং জমিটির পরিসীমা 40 মিটার। জমিটির দৈর্ঘ্য ও প্রস্থ নির্ণয় কর।

ফ্রান্সের বিখ্যাত গণিতবিদ রেনে দেকার্তে (Rene Descartes 1596-1650) সর্বপ্রথম স্থানাঙ্কের ধারণা দেন। তিনি দুটি পরস্পরছেদী লম্বরেখার সাপেক্ষে বিন্দুর অবস্থান ব্যাখ্যা করেন।

একটি শ্রেণিকক্ষে একক আসনবিন্যাসে একজন শিক্ষার্থীর অবস্থান কোথায় জানতে হলে অনুভূমিক রেখা বা শয়ান রেখা বরাবর কোথায় আছে এবং উল্লম্ব রেখা বা খাড়া রেখা বরাবর কোথায় আছে তা জানা দরকার।

ধরি, শ্রেণিকক্ষে একজন শিক্ষার্থী লিজা (L)-এর অবস্থান জানতে চাই। লিজার অবস্থানকে একটি বিন্দু (•) হিসেবে বিবেচনা করা যায়। চিত্রে লক্ষ করি, লিজা একটি নির্দিষ্ট বিন্দু থেকে অনুভূমিক রেখা OX বরাবর 3 একক দূরে M বিন্দুতে এবং সেখান থেকে উল্লম্ব রেখা OY এর সমান্তরাল রেখা বরাবর উপরদিকে 2 একক দূরে L বিন্দুতে অবস্থান করছে। তার এ অবস্থানকে (3, 2) দ্বারা প্রকাশ করা হয়।

ছক কাগজে সমান দূরে পরস্পরছেদী সমান্তরাল সরলরেখা দ্বারা ছোটো ছোটো বর্গে বিভক্ত করা থাকে। ছক কাগজে কোনো বিন্দুর অবস্থান দেখানোকে বা কোনো বিন্দু স্থাপন করাকে বিন্দু পাতন বলে। বিন্দু পাতনের জন্য সুবিধামতো দুটি পরস্পর লম্ব সরলরেখা নেওয়া হয়। চিত্রে XOX'ও YOY' রেখাদ্বয় পরস্পর লম্বভাবে ০ বিন্দুতে ছেদ করেছে। O বিন্দুকে বলা হয় মূলবিন্দু। অনুভূমিক রেখা XOX' কে x-অক্ষ এবং উল্লম্ব রেখা YOY' কেy-অক্ষ বলা হয়।

প্রধানত ছক কাগজের ক্ষুদ্রতম বর্গক্ষেত্রের বাহুর দৈর্ঘ্যকে একক হিসেবে ধরা হয়। সাধারণভাবে যেকোনো বিন্দুর স্থানাঙ্ককে (x, y) লেখা হয়। X-কে বলা হয় বিন্দুটির x-স্থানাঙ্ক বা ভুজ এবং y-কে বলা হয় বিন্দুটির -স্থানাঙ্ক বা কোটি। স্পষ্টতই মূলবিন্দু O এর স্থানাঙ্ক হবে (0,0)।

মূলবিন্দু থেকে x-অক্ষের ডানদিক ধনাত্মক দিক ও বামদিক ঋণাত্মক দিক। আবার, মূলবিন্দু থেকে -অক্ষের উপরের দিক ধনাত্মক দিক ও নিচের দিক ঋণাত্মক দিক। ফলে ছকটি অক্ষদ্বয় দ্বারা চারটি ভাগে বিভক্ত হয়েছে। এইভাগ চারটি ঘড়ির কাঁটার ঘূর্ণনের বিপরীত দিক অনুযায়ী ১ম, ২য়, ৩য় ও ৪র্থ চতুর্ভাগ হিসেবে পরিচিত। প্রথম চতুর্ভাগে যেকোনো বিন্দুর x স্থানাঙ্ক ও স্থানাঙ্ক উভয়ই ধনাত্মক, দ্বিতীয় চতুর্ভাগে যেকোনো বিন্দুর X স্থানাঙ্ক ঋণাত্মক ও y স্থানাঙ্ক ধনাত্মক, তৃতীয় চতুর্ভাগে যেকোনো বিন্দুর X স্থানাঙ্ক ঋণাত্মক ও y স্থানাঙ্ক ঋণাত্মক এবং চতুর্থ চতুর্ভাগে যেকোনো বিন্দুর X স্থানাঙ্ক ধনাত্মক ও y স্থানাঙ্ক ঋণাত্মক।

পূর্বের অনুচ্ছেদে আলোচিত লিজার অবস্থান (3, 2) নির্ণয় করার জন্য প্রথমে x-অক্ষ বরাবর ডানদিকে 3 একক দূরত্বে যেতে হবে। তারপর সেখান থেকে খাড়া উপর দিকে 2 একক দূরত্বে যেতে হবে। তা হলে লিজার অবস্থান L বিন্দুর স্থানাঙ্ক হবে (3,2)। অনুরূপভাবে চিত্রে P বিন্দুর স্থানাঙ্ক (-2,4)।

উদাহরণ ১। ছক কাগজে নিচের প্রথম চারটি বিন্দু স্থাপন করে তীর চিহ্ন অনুযায়ী যোগ কর: (3, 2) $\to$ (6, 2) $\to$ (6, 4) $\to$ (3, 4) । চিত্রটির জ্যামিতিক আকৃতি কী হবে?

সমাধান: ধরি, বিন্দু চারটি যথাক্রমে A, B, C, D। অর্থাৎ, A(3, 2) B(6, 2) C(6,4) এবং D(3, 4) । ছক কাগজে উভয় অক্ষে ক্ষুদ্রতম বর্গক্ষেত্রের প্রতি বাহুর দৈর্ঘ্যকে একক ধরি। A বিন্দুটি স্থাপন করতে মূলবিন্দু O থেকে x-অক্ষের ডানদিক বরাবর 3টি ছোট বর্গের বাহুর সমান দূরে গিয়ে উপরের দিকে ২টি ছোটো বর্গের বাহুর সমান উঠে গেলে যে বিন্দুটি পাওয়া যাবে, তা A বিন্দু। অনুরূপভাবে প্রদত্ত অবশিষ্ট বিন্দুসমূহ স্থাপন করি। তারপর A $\to$ B $\to$ C $\to$ D $\to$ A এভাবে বিন্দুগুলো যোগ করি। এতে ABCD চিত্রটি পাওয়া গেল। দেখা যায় যে, ABCD চিত্রটি একটি আয়ত।

কাজ: চিত্র থেকে তোমরা Q, R, S, T বিন্দুর স্থানাঙ্ক নির্ণয় কর।

লেখচিত্রের সাহায্যে সহজেই সমীকরণের সমাধান বের করা যায়। মনে করি, 2x - 5 = 0 সমীকরণটি সমাধান করতে হবে। সমীকরণের বামপক্ষ 2x - 5 রাশিতে x-এর বিভিন্ন মান বসালে রাশিটির বিভিন্ন মান পাওয়া যায়। লেখচিত্রে প্রতিটি X কে ভুজ এবং রাশিটির মানকে কোটি ধরে একটি করে বিন্দু পাওয়া যাবে। বিন্দুগুলো যোগ করে একটি সরলরেখা অঙ্কিত হবে। সরলরেখাটি যে বিন্দুতে x অক্ষকে ছেদ করে, সেই বিন্দুর ভুজই নির্ণেয় সমাধান। কেননা, x-এর এই মানের জন্য রাশিটির মান 0 হয়, যা সমীকরণের ডানপক্ষের মানের সমান হয়। এ ক্ষেত্রে সমীকরণটির সমাধান $x=\frac{5}{2}$।

উদাহরণ ২। 3x - 6 = 0 সমাধান কর এবং লেখচিত্রে সমাধান প্রদর্শন কর।

সমাধান: 3x - 6 = 0

বা, 3x = 6 [পক্ষান্তর করে]

বা, $\frac{3x}{3}=\frac{6}{3}$[উভয়পক্ষকে 3 দ্বারা ভাগ করে]

বা, x = 2

∴ সমাধান: x = 2

লেখচিত্র অঙ্কন: প্রদত্ত সমীকরণ 3x-6=0

x এর কয়েকটি মান নিয়ে 3x - 6 এর অনুরূপ মান বের করি এবং নিচের ছকটি তৈরি করি:

লেখচিত্র অঙ্কনের জন্য তিনটি বিন্দু (2,0), (5,9) ও (6,12) নেওয়া হলো।

মনে করি, পরস্পর লম্ব রেখা XOX' ও YOY' যথাক্রমে x-অক্ষ ও y-অক্ষ এবং O মূলবিন্দু।

ছক কাগজে উভয় অক্ষে ক্ষুদ্রতম বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্যকে একক ধরে (2,0), (5,9), (6,12) বিন্দুগুলো স্থাপন করি। তারপর বিন্দুগুলো পরপর সংযোগ করি। লেখচিত্রে একটি সরলরেখা পাই। সরলরেখাটি x-অক্ষকে (2,0) বিন্দুতে ছেদ করে। বিন্দুটির ভুজ হলো 2। সুতরাং প্রদত্ত সমীকরণের সমাধান x = 2 ।

উদাহরণ ৩। লেখচিত্রের সাহায্যে সমাধান কর: 3x - 4 = - x + 4

সমাধান: প্রদত্ত সমীকরণ 3x - 4 = - x + 4

x এর কয়েকটি মান নিয়ে 3x - 4 এর অনুরূপ মান বের করি এবং পাশের ছক-১ তৈরি করি:

∴ 3x - 4 এর লেখের উপর তিনটি বিন্দু (0,-4), (2,2), (4,8) নিই।

ছক-১

আবার, x এর কয়েকটি মান নিয়ে - x + 4 এর অনুরূপ মান বের করি এবং পাশের ছক-২ তৈরি করি:

∴ -x + 4 এর লেখের উপর তিনটি বিন্দু (0,4), (2,2), (4,0) নিই।

মনে করি, পরস্পর লম্ব রেখা XOX' ও YOY' যথাক্রমে x-অক্ষ ও ৮-অক্ষ এবং মূলবিন্দু। এখন, ছক-১ এ প্রাপ্ত (0,-4), (2,2), (4, 8) বিন্দু তিনটি স্থাপন করি এবং এদের পরপর সংযোগ করি।

ছক-২

(0,4), (2, 2), (4,0) বিন্দু তিনটি স্থাপন করি ও এদের পরপর সংযোগ করি। এক্ষেত্রেও লেখচিত্রে একটি সরলরেখা পাই।

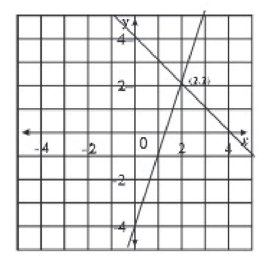
লক্ষ করি, সরলরেখা দুটি পরস্পর (2,2) বিন্দুতে ছেদ করেছে। ছেদবিন্দুতে 3x-43-x+4 এর মান পরস্পর সমান। সুতরাং, প্রদত্ত সমীকরণের সমাধান হলো (2, 2) বিন্দুতে ভুজের মান, অর্থাৎ x = 2 ।

১। $\frac{x}{3}-3=0$ সমীকরণের মূল নিচের কোনটি?

ক. -9 খ.-3 গ. 3 ঘ. 9

২। একটি ত্রিভুজের বাহু তিনটির দৈর্ঘ্য (x + 1) সে.মি., (x + 2) সে.মি. ও (x + 3) সে.মি. (x > 0) । ত্রিভুজটির পরিসীমা 15 সে.মি. হলে, x এর মান কত?
(ক) 3 সে.মি. (খ) 6 সে.মি. (গ) ৪ সে.মি. (ঘ) 9 সে.মি.

৩। কোন সংখ্যার এক-চতুর্থাংশ 4 এর সমান হবে?
(ক) 16 (খ) 4 (গ) $\frac{1}{4}$(ঘ) $\frac{1}{6}$

৪। (2,-2) বিন্দুটি কোন চতুর্ভাগে অবস্থিত?
(ক) প্রথম (খ) দ্বিতীয় (গ) তৃতীয় (ঘ) চতুর্থ

৫। y অক্ষ বরাবর কোন বিন্দুর ভুজ কত?
(ক) 0
(খ) 1
(গ) X
(ঘ) y

৬। দুটি সংখ্যার বিয়োগফল y, বড়ো সংখ্যাটি z হলে, ছোটো সংখ্যাটি কত?
(ক) z - y
(খ) z + y
(গ) - y - z
(ঘ) - z + y

৭। $\frac{ab}{xy}$এর সমতুল ভগ্নাংশ নিচের কোনটি?

(ক) $\frac{abc}{xyz}$ (খ) $\frac{a^{2}b}{x^{2}y}$

(গ) $\frac{2ab }{2xy}$ (ঘ) $\frac{a{b}^2}{x{y}^2}$

৮। 3x + 1 = 0 সমীকরণের ঘাত কত?

(ক)$-\frac{1}{3}$ (খ) $\frac{1}{3}$

(গ) 1 (ঘ) 3

৯। কোন সংখ্যার সাথে 5 যোগ করলে 15 হবে?
(ক) -20
(খ) 10
(গ) -10
(ঘ) 20

১০। x এর কোন মান 4x+1=2x+7 সমীকরণকে সিদ্ধ করে?
(ক) 0
(খ) 2
(গ) 3
(ঘ) 4

১১। চিত্র থেকে নিচের ছকটি পূরণ কর:
(উভয় অক্ষে ক্ষুদ্রতম বর্গক্ষেত্রের বাহুর দৈর্ঘ্যকে একক ধরে)

১২। নিচের বিন্দুগুলো ছক কাগজে স্থাপন করে তীরচিহ্ন অনুযায়ী যোগ কর ও চিত্রটির জ্যামিতিক নামকরণ কর।
(ক) (2, 2) $\to$ (6, 2) $\to$ (6, 6) $\to$ (2, 6) $\to$ (2, 2)
(খ) (0, 0)$\to$ (- 6, - 6)$\to$ (8, 6) $\to$ (0, 0)

১৩। সমাধান কর এবং সমাধান লেখচিত্রে দেখাও।
(ক) x - 4 = 0
(খ) 2x + 4 = 0
(গ) x + 3 = 8
(ঘ) 2x + 1 = x - 3
(ঙ) 3x + 4 = 5x

১৪। একটি ত্রিভুজের তিন বাহুর দৈর্ঘ্য (x+2) সে.মি., (x+4) সে.মি. ও (x+6) সে.মি. (x > 0)
এবং ত্রিভুজটির পরিসীমা 18 সে.মি.।
ক. প্রদত্ত শর্তানুযায়ী আনুপাতিক চিত্র আঁক।
খ. সমীকরণ গঠন করে সমাধান কর।
গ. সমাধানের লেখচিত্র আঁক।

১৫। ঢাকা ও আরিচার মধ্যবর্তী দূরত্ব 77 কি.মি.। একটি বাস ঘণ্টায় 30 কি.মি. বেগে ঢাকা থেকে আরিচার পথে রওনা দিল। অপর একটি বাস ঘণ্টায় 40 কি.মি. বেগে আরিচা থেকে ঢাকার পথে একই সময়ে রওনা দিল ও বাস দুটি ঢাকা থেকে x কি.মি. দূরে মিলিত হলো।
ক. বাস দুটি আরিচা থেকে কত দূরে মিলিত হবে তা x এর মাধ্যমে প্রকাশ কর।
খ. x এর মান নির্ণয় কর।
গ. গন্তব্যস্থানে পৌঁছাতে কোন বাসের কত সময় লাগবে?